Prediction of single-well-constrained recoverable reserves in beach bar sand reservoir using different fracturing methods
-
摘要: 单井控制可采储量是评价滩坝砂油藏开发是否经济可行的重要指标。由于未动用特低渗透滩坝砂油藏存在压敏效应、启动压力梯度、不同压裂方式等特征，难以应用常规的单井控制可采储量预测方法进行预测。基于典型区块静、动态数据，建立直井分层压裂油藏数值模拟模型，通过历史拟合确定启动压力梯度及压敏效应表征公式中的系数，并分析压敏效应和启动压力梯度对生产动态的影响。在此基础上，分析不同油藏参数和开发参数对直井分层压裂弹性开发单井控制可采储量的影响，确定单井控制可采储量的主控因素依次为：压力系数、渗透率、含油饱和度、有效厚度、孔隙度、压裂缝长、集中度和黏度；通过多元回归方式建立直井分层压裂弹性开发下单井控制可采储量与主控因素之间的计算公式，经与实际生产井数据对比，相对误差为4.58%，说明公式具有较高的精度，能够满足矿场要求。进一步建立直井体积压裂、水平井多段压裂和水平井体积压裂弹性开发单井控制可采储量与油藏参数之间的预测公式，研究结果为评价滩坝砂油藏动用潜力提供基础。Abstract: Single-well-constrained recoverable reserve is an important index to evaluate whether the development of beach bar sand reservoir is economically feasible. Due to the characteristics of pressure sensitive effect, start-up pressure gradient and different fracturing methods, it is difficult to apply the conventional prediction method to single-well-constrained recoverable reserve in undeveloped ultra-low permeability beach bar sand reservoirs. In this paper, based on the static and dynamic data of typical blocks, a numerical simulation model of vertical well stratified fracturing was established. The coefficients in the characterization formula of start-up pressure gradient and pressure-sensitive effect were determined by history fitting, and the influences of pressure-sensitive effect and start-up pressure gradient on production performance were analyzed. On this basis, the influence of different reservoir parameters and development parameters on the single-well-constrained recoverable reserves of elastic development with vertical-well stratified fracturing was analyzed. The main factors of single-well-constrained recoverable reserves were determined as follows: pressure coefficient, permeability, oil saturation, effective thickness, porosity, fracture length, concentration and viscosity. A vertical-well stratified fracturing model was established by multiple regression. Compared with the data from actual production wells, the relative error was 4.58%, which showed that the formula had a high accuracy and could meet the requirements of mines. Furthermore, some prediction formulas between the single-well-constrained recoverable reserves and the reservoir parameters corresponding to the volume fracturing of vertical wells, the multi-stage fracturing of horizontal wells and the volume fracturing of horizontal wells were established. The results provided a basis for evaluating the production potential of beach bar sand reservoirs.
-
滩坝砂油藏具有储层物性差、纵向层多层薄、层间非均质性强、储量丰度低的特点，常规投产油井自然产能低，压裂开发是提高滩坝砂油藏开发效果的主要技术[1-5]。
单井控制可采储量是评价滩坝砂油藏开发是否经济可行的重要指标。目前低渗透滩坝砂油藏多采用弹性开发，受启动压力梯度、压敏效应、压裂参数等影响，单井控制可采储量计算不能采用基于常规的综合压缩系数的计算方法。在对低渗透油藏单井控制可采储量计算研究中，部分学者以渗流力学模型为基础，从活塞流到非活塞流计算公式，利用渗流力学公式推导产能半解析解，但该方法难以考虑不同油藏参数及压裂参数的影响[6-8]。SLIDER[9]采用经验公式法，但需要使用大量油田生产数据进行统计回归。水驱特征曲线法、产量递减法等是利用产水量、产油量等动态数据并通过回归方法得出相关公式，并以此为基础预测可采储量[10-18]，但是此方法只适用于水驱油藏的后期，并依赖于大量生产动态数据。
油藏数值模拟技术可以综合考虑储层非均质性、启动压力梯度、压敏效应等多种因素的影响。为此，本文针对滩坝砂油藏特征，考虑启动压力梯度及压敏效应的影响，以典型区块静态数据和动态数据为基础，采用油藏数值模拟技术建立与实际油藏特征一致的数值模型，计算分析不同压裂方式单控可采储量及主控因素，应用多元回归方法建立不同压裂方式对应的单井控制可采出量预测模型，以期为滩坝砂油藏的有效开发提供技术支持。
1. 考虑启动压力梯度和压敏效应的油藏数值模型
1.1 油藏数值模拟基础模型
根据滩坝砂油藏Y区块油藏建立油藏数值模拟基础模型。该区块油层中部深度为3 714.1 m，原始地层压力为52.59 MPa，压力系数为1.42，有效厚度为23.5 m，地层原油黏度为0.76 mPa·s，原油的体积系数为1.331，压缩系数为1.89 ×10-3 MPa-1，饱和压力为15.98 MPa。结合该区块开发方案中的井网设计，在模型中单井控制面积设置为440 m×500 m。依据实际井压裂数据，采用直井分层压裂进行开发，设置压裂半缝长为145 m，缝宽为2.9 cm。
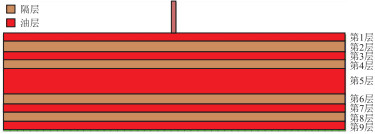
针对滩坝砂单砂体薄、呈砂泥岩互层状的特点，纵向上模型设置为9个薄层，其中第1，3，5，7，9层为产油层，第2，4，6，8层为泥岩隔层(图 1)。为突出主力层与非主力层的差异，提出了集中度的概念，即油藏主力层有效厚度与油层总有效厚度的比值，其计算公式为：
g=h/hz (1) 式中：g为集中度；h为主力层有效厚度，m；hz为油层总厚度，m。
模型中设置主力产油层为第5层，有效厚度为8 m，其余非主力产油层有效厚度为4 m。因此该级差模型的集中度为0.34。
1.2 启动压力梯度和压敏效应模型确定及设置
由于压敏效应的影响，储层近井地带渗透率下降，渗流阻力增大，使油井产量降低[19]。压敏表征公式为：
ki=k0e∂(pi−p0) (2) 式中：pi为目前地层压力，MPa；ki为pi下的渗透率，10-3 μm2；p0为原始地层压力，MPa；k0为原始地层压力下的渗透率，10-3 μm2；∂为压敏系数，MPa-1。
基于公式(2)可得出渗透率与地层压力的关系，将其以表的形式插入所建立的数值模拟模型中，并通过线性插值的方式赋予每个网格渗透率与地层压力的变化关系以表征压敏效应。
特低渗滩坝砂储层孔喉细微，渗流表现为非达西渗流特征，因此，启动压力梯度不可忽略[20]，其表征公式为：
G=A(kμ)B (3) 式中：G为启动压力梯度，MPa/m；A为系数，通常在2~3之间；B为流度的相关系数，常数；k为渗透率，10-3 μm2；μ为黏度，mPa·s。
在数模软件中通过网格设置为不同的区，并对流体在不同区之间流动设置“门限压力”，需要克服“门限压力”流体才能流动，以此来实现启动压力梯度的等效模拟[21]。
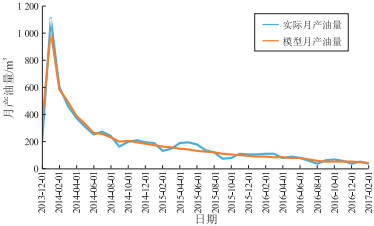
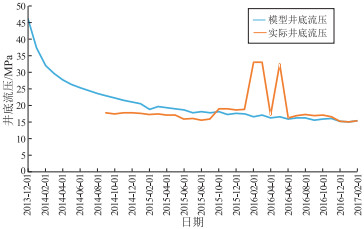
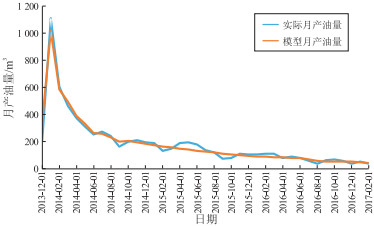
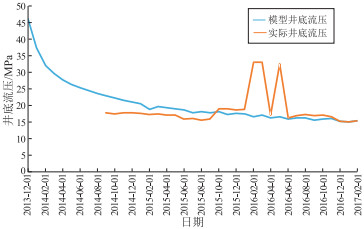
在数值模型中，通过历史拟合确定启动压力梯度数学模型的相关参数以及压敏公式中的压敏系数[22-23]。拟合具体结果如图 2、图 3所示，模拟计算得出的累积产油量为7 203 m3，实际产油量为7 312 m3，相对误差为1.5%，模拟结束时生产的井底流压与实际生产的井底流压都为15.3 MPa。
通过历史拟合得到压敏公式及启动压力梯度的数学模型为：
压敏表征公式：
ki=k0e0.01(pi−p0) (4) 启动压力梯度表征公式：
G=2.1(kμ)1.7145 (5) 1.3 压敏系数及启动压力梯度对渗流场的影响
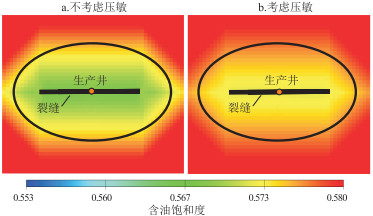
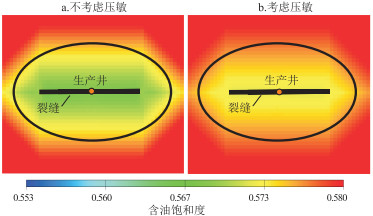
在相同的工作制度下，油井的井底流压通过阶梯式降压降至饱和压力附近。图 4为考虑压敏效应与不考虑压敏效应的含油饱和度场图，可以看出考虑压敏效应的井筒及裂缝附近储层含油饱和度更高。因为井筒及裂缝附近的储层由于压敏效应的影响，地层压力下降导致渗透率降低，剩余油更加不易开采。
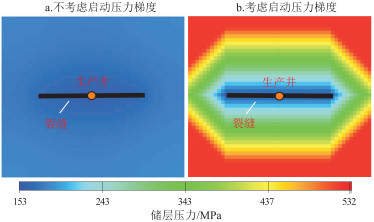
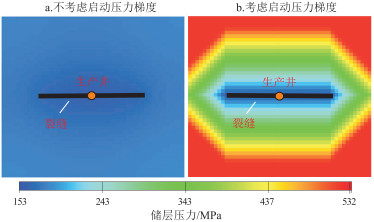
图 5为考虑启动压力梯度与不考虑启动压力梯度的压力场图，可以看出，在启动压力梯度的影响下，油井附近会存在一定的能量动用边界和泄油半径。在驱动压力梯度小于启动压力梯度的区域，储层流体无法流动。因此，在动用边界以外的区域剩余油在弹性开发下无法动用。
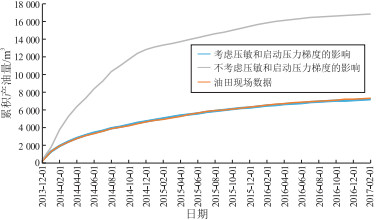
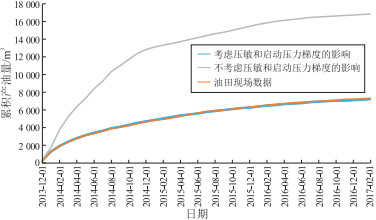
从累积产油量对比曲线(图 6)可以看出，不考虑启动压力梯度及压敏效应的累积产油量明显偏高，考虑启动压力梯度及压敏效应的累积产油量曲线与实际累积产油量曲线更加契合，说明考虑启动压力梯度及压敏效应的数值模拟模型更能反映现场油藏的生产动态。
图 6 油田现场数据与模型计算累积产油量对比Figure 6. Comparison of field data and model calculated cumulative oil productions2. 单井控制可采储量主控因素
影响滩坝砂单井控制可采储量的地质因素主要包括渗透率、有效厚度、原油黏度、含油饱和度、集中度、压力系数以及岩石压缩系数等，开发因素主要为压裂缝长。
基于建立的数值模拟基础模型，在其他条件不变的情况下，研究单因素对单井控制可采储量的影响程度。设置模型各影响因素的基准值如下：渗透率4×10-3 μm2，有效厚度24 m，黏度0.76 mPa·s，含油饱和度0.573，孔隙度0.107，压力系数1.42，压缩系数1 MPa-1，集中度0.32，压裂缝长145 m。
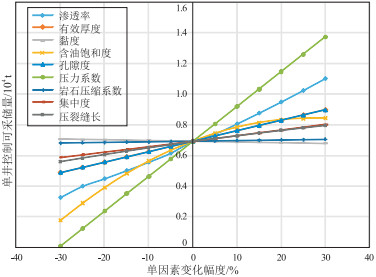
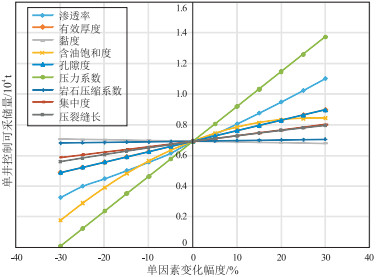
通过油藏数值模拟技术计算分析各影响因素在变化±30%范围内对应的直井分层压裂单井控制可采储量，如表 1和图 7所示。可以看出，弹性开发单井控制可采储量与渗透率、厚度、含油饱和度、孔隙度、压力系数、集中度、岩石压缩系数及压裂缝长呈正相关关系，与黏度呈负相关关系。各个因素在±30%范围内，对单井控制可采储量的敏感程度从高到低依次为：压力系数、渗透率、含油饱和度、有效厚度、孔隙度、压裂缝长、集中度、黏度和岩石压缩系数。由于岩石压缩系数对单井控制可采储量的影响较小，在后面的分析中不再考虑。
表 1 单井控制可采储量随各油藏参数因素变化状况Table 1. Variation of single-well-constrained recoverable reserves with various reservoir parameters变化幅度/% 单井控制可采储量评估结果/104 t 渗透率 有效厚度 黏度 含油饱和度 孔隙度 压力系数 压缩系数 集中度 压裂缝长 -30 0.325 0.488 0.708 0.177 0.489 0.009 0.681 0.588 0.559 -25 0.399 0.522 0.705 0.289 0.523 0.123 0.683 0.605 0.583 -20 0.448 0.556 0.703 0.391 0.557 0.237 0.685 0.623 0.606 -15 0.501 0.591 0.701 0.483 0.591 0.351 0.687 0.640 0.629 -10 0.556 0.625 0.698 0.564 0.625 0.464 0.689 0.658 0.650 -5 0.615 0.659 0.696 0.634 0.66 0.578 0.691 0.675 0.671 0 0.693 0.693 0.693 0.693 0.693 0.693 0.693 0.693 0.693 5 0.740 0.728 0.691 0.745 0.728 0.806 0.696 0.711 0.711 10 0.806 0.762 0.689 0.785 0.762 0.920 0.698 0.729 0.730 15 0.876 0.796 0.686 0.815 0.796 1.034 0.700 0.748 0.748 20 0.949 0.83 0.684 0.834 0.83 1.148 0.702 0.766 0.765 25 1.024 0.865 0.682 0.843 0.864 1.262 0.704 0.784 0.782 30 1.102 0.899 0.679 0.844 0.898 1.375 0.706 0.803 0.798 变化30%与-30%的差额 0.777 0.411 0.029 0.667 0.409 1.366 0.025 0.215 0.239 
图 7 各参数变化幅度对应的单井控制可采储量变化曲线Figure 7. Variation curves of single-well-constrained recoverable reserves corresponding to the variation range of each parameter3. 单井控制可采储量预测模型建立及验证
3.1 单井控制可采储量预测模型建立
基于直井分层压裂单井控制可采储量主控因素，通过回归方程表征单井控制可采储量变量受一个或多个油藏参数影响的程度[24-26]。在前面分析所产生的数据基础上，增加样本数量到196个，通过对不同回归方程形式的精度分析，确定的多元回归公式为：
N1=0.015(k0.924×h0.648×S1.0570×φ0.823×g0.449×P1.781i×μ−0.145×T0.563) (6) 式中：N1为弹性开发单井控制可采储量，104 t；S0为含油饱和度；φ为孔隙度；Pi为压力系数；T为半缝长，m。
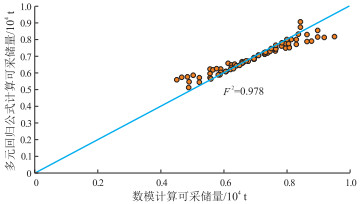
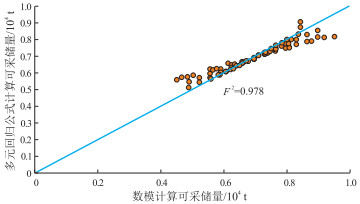
公式(6)的参数取值范围为：储层渗透率(1~8)×10-3 μm2，有效厚度5~25 m，含油饱和度0.46~0.64，孔隙度0.10~0.15，集中度0.1~0.5，压力系数1.2~1.6，黏度0.76~6.00mPa·s，半缝长80~185 m。在该范围内，回归拟合度高，F2 =0.978(图 8)。基于建立的单井控制可采储量多元回归公式(6)，在合理的油藏参数及开发参数取值范围内，可预测出不同油藏条件下直井分层压裂的单井控制可采储量。
3.2 单井控制可采储量预测模型实例验证
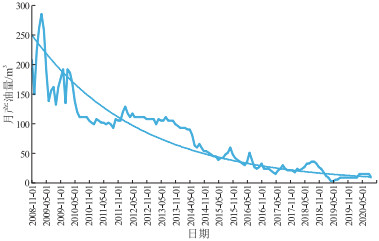
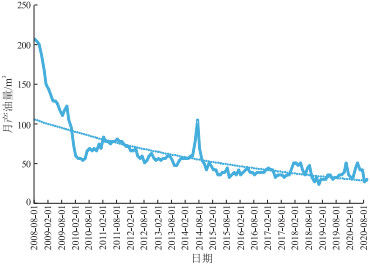
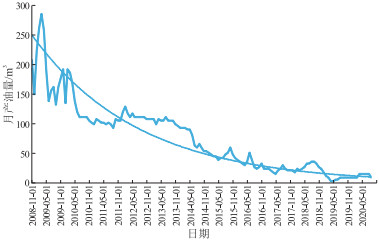
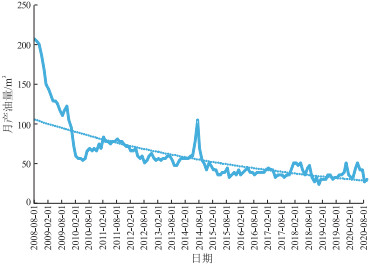
选取F区滩坝砂油藏5口典型井的生产数据进行分析，根据每口井的产量递减曲线得到井的实际递减率，进而预测得到每口井的实际单井控制可采储量，其中两口井的产量变化曲线见图 9和图 10。
根据5口井的油藏参数和开发参数代入公式(7)，可计算出其单井控制可采储量。表 2为5口井的实际单井控制可采储量与所建公式预测结果的对比，可以看出多元回归计算所得的可采储量与实际生产的可采储量的平均相对误差为4.58%，说明直井分层压裂单井控制可采储量多元回归模型具有较高的精度，能够满足矿场要求。
表 2 单井控制可采储量对比Table 2. Comparison of single-well-constrained recoverable reserves井号 渗透率/10-3 μm2 有效厚度/m 含油饱和度 孔隙度 集中度 目前累计产油量/104 t 单井控制可采储量/104 t 相对误差/% 预测值 多元回归计算值 FXX4-X9 5.87 12.1 0.380 0.143 0.10 0.85 0.91 0.90 1.099 FXX1-X8 14.40 8.5 0.523 0.142 0.36 1.34 1.36 1.28 5.882 FXX7-X6 9.11 11.4 0.476 0.141 0.38 1.01 1.02 1.05 2.941 FXX7-X2 5.43 25.8 0.370 0.118 0.20 0.62 0.66 0.61 7.576 FXX4-X6 4.85 11.4 0.392 0.144 0.30 0.34 0.37 0.39 5.405 4. 不同压裂方式下单井控制可采储量预测模型
基于上述滩坝砂油藏直井分层压裂弹性开发单井控制可采储量的研究方法和所建油藏数值模拟模型，分别建立直井体积压裂、水平段多段压裂、水平井体积压裂3种压裂方式下弹性开发单井控制可采储量多元回归模型。其中，直井体积压裂弹性开发单井控制可采储量多元回归方程为：
N2=0.204(k0.6×h0.724×S1.1930×φ0.917×g0.08×P1.67i×μ−0.005×T0.154) (7) 式中：N2为直井体积压裂弹性开发单井控制可采储量，104 t。
水平井多段压裂弹性开发单井控制可采储量多元回归方程为：
N3=0.001(k0.785×h0.049×S0.8960×φ0.829×g1.271×P2.464i×μ−0.006×T0.616×H0.886) (8) 式中：H为水平井水平井筒长度，m；N3为水平井多段压裂弹性开发单井控制可采储量，104 t。
水平井体积压裂弹性开发单井控制可采储量多元回归方程为：
N4=0.001(k0.6×h0.1×S0.910×φ0.856×g0.573×P2.499i×μ−0.016×T0.612×H0.846) (9) 式中：N4为水平井体积压裂弹性开发单井控制可采储量，104 t。
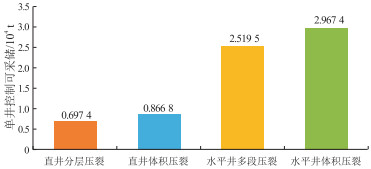
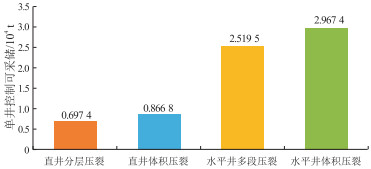
公式(8)和(9)中水平井水平井筒长度取值范围为700~1 300 m，其余参数取值范围同公式(6)。在相同的油藏参数(渗透率4.93×10-3 μm2，有效厚度11.53 m，含油饱和度0.573，压力系数1.4，孔隙度0.125，黏度0.76 mPa·s，集中度0.4)和开发参数(半缝长150 m，水平段长度1 000 m)下，利用公式(6)—(9)计算出不同压裂方式下的单井控制可采储量(图 11)。可以看出，基于相同的储层地质参数，采用水平井多段压裂获得的单井控制可采储量比直井分层压裂高出1.822 1×104 t；体积压裂相比常规压裂也能增加单井控制可采储量。因此，随着压裂开发技术的进步，原本难动用的特低渗油藏会变得更有开发价值。
图 11 不同井型及压裂规模单井控制可采储量对比Figure 11. Comparison of single-well-constrained recoverable reserves of different well types and fracturing scales5. 结论
(1) 在建立滩坝砂油藏数值模拟模型时，考虑了启动压力梯度及压敏效应的影响，模拟计算的产油量与实际产油量误差控制在1.5%，模拟结果能反映矿场的实际生产状况。
(2) 计算分析了油藏参数和开发参数在变化±30%范围对应的单井控制可采储量，确定了弹性开发单井控制可采储量的主控因素依次为：压力系数、渗透率、含油饱和度、有效厚度、孔隙度、压裂缝长、集中度和黏度。
(3) 采用多元回归方法建立了滩坝砂油藏不同压裂方式下单井控制可采储量的计算公式，经与实际生产井生产数据对比，相对误差在5%以内，具有较高的精度，为评价滩坝砂油藏动用潜力奠定了基础。
致谢: 本文在撰写过程中得到中国石油大学(华东)崔传智教授的帮助，审稿专家和编辑部老师也对本文提出了建设性意见，在此致以衷心感谢！ -
图 6 油田现场数据与模型计算累积产油量对比
Figure 6. Comparison of field data and model calculated cumulative oil productions
图 7 各参数变化幅度对应的单井控制可采储量变化曲线
Figure 7. Variation curves of single-well-constrained recoverable reserves corresponding to the variation range of each parameter
图 11 不同井型及压裂规模单井控制可采储量对比
Figure 11. Comparison of single-well-constrained recoverable reserves of different well types and fracturing scales
表 1 单井控制可采储量随各油藏参数因素变化状况
Table 1. Variation of single-well-constrained recoverable reserves with various reservoir parameters
变化幅度/% 单井控制可采储量评估结果/104 t 渗透率 有效厚度 黏度 含油饱和度 孔隙度 压力系数 压缩系数 集中度 压裂缝长 -30 0.325 0.488 0.708 0.177 0.489 0.009 0.681 0.588 0.559 -25 0.399 0.522 0.705 0.289 0.523 0.123 0.683 0.605 0.583 -20 0.448 0.556 0.703 0.391 0.557 0.237 0.685 0.623 0.606 -15 0.501 0.591 0.701 0.483 0.591 0.351 0.687 0.640 0.629 -10 0.556 0.625 0.698 0.564 0.625 0.464 0.689 0.658 0.650 -5 0.615 0.659 0.696 0.634 0.66 0.578 0.691 0.675 0.671 0 0.693 0.693 0.693 0.693 0.693 0.693 0.693 0.693 0.693 5 0.740 0.728 0.691 0.745 0.728 0.806 0.696 0.711 0.711 10 0.806 0.762 0.689 0.785 0.762 0.920 0.698 0.729 0.730 15 0.876 0.796 0.686 0.815 0.796 1.034 0.700 0.748 0.748 20 0.949 0.83 0.684 0.834 0.83 1.148 0.702 0.766 0.765 25 1.024 0.865 0.682 0.843 0.864 1.262 0.704 0.784 0.782 30 1.102 0.899 0.679 0.844 0.898 1.375 0.706 0.803 0.798 变化30%与-30%的差额 0.777 0.411 0.029 0.667 0.409 1.366 0.025 0.215 0.239 
下载: 导出CSV
表 2 单井控制可采储量对比
Table 2. Comparison of single-well-constrained recoverable reserves
井号 渗透率/10-3 μm2 有效厚度/m 含油饱和度 孔隙度 集中度 目前累计产油量/104 t 单井控制可采储量/104 t 相对误差/% 预测值 多元回归计算值 FXX4-X9 5.87 12.1 0.380 0.143 0.10 0.85 0.91 0.90 1.099 FXX1-X8 14.40 8.5 0.523 0.142 0.36 1.34 1.36 1.28 5.882 FXX7-X6 9.11 11.4 0.476 0.141 0.38 1.01 1.02 1.05 2.941 FXX7-X2 5.43 25.8 0.370 0.118 0.20 0.62 0.66 0.61 7.576 FXX4-X6 4.85 11.4 0.392 0.144 0.30 0.34 0.37 0.39 5.405
下载: 导出CSV
-
[1] 郭鸣黎, 陈艳, 郑振恒, 等. 致密油藏可采储量概率快速评估方法: 以红河油田长8油藏为例[J]. 石油实验地质, 2021, 43(1): 154-160. doi: 10.11781/sysydz202101154GUO Mingli, CHEN Yan, ZHENG Zhenheng, et al. Rapid evaluation of probable recoverable reserves in tight reservoirs: a case study of Chang 8 reservoir (eighth member of Yanchang Formation) in Honghe oil field[J]. Petroleum Geology & Experiment, 2021, 43(1): 154-160. doi: 10.11781/sysydz202101154 [2] 赵淑霞, 于红军. 滩坝砂特低渗透油藏经济动用技术研究与实践[J]. 油气地质与采收率, 2009, 16(2): 96-98. https://www.cnki.com.cn/Article/CJFDTOTAL-YQCS200902033.htmZHAO Shuxia, YU Hongjun. Economical production technologies research and application of ultra low permeability beach-bar sand reservoirs[J]. Petroleum Geology and Recovery Efficiency, 2009, 16(2): 96-98. https://www.cnki.com.cn/Article/CJFDTOTAL-YQCS200902033.htm [3] 宋彦男, 曲占庆, 肖春金. 低渗透滩坝砂储层压裂评价决策方法[J]. 天然气勘探与开发, 2016, 39(2): 50-53. https://www.cnki.com.cn/Article/CJFDTOTAL-TRKT201602011.htmSONG Yannan, QU Zhanqing, XIAO Chunjin. Decision methods for evaluating low-permeability beach-bar sandstone reservoirs developed by hydraulic fracturing[J]. Natural Gas Exploration and Development, 2016, 39(2): 50-53. https://www.cnki.com.cn/Article/CJFDTOTAL-TRKT201602011.htm [4] 刘小波. CO2混相驱技术在特低渗透滩坝砂油藏的开发实践及效果评价[J]. 油气地质与采收率, 2020, 27(3): 113-119. https://www.cnki.com.cn/Article/CJFDTOTAL-YQCS202003016.htmLIU Xiaobo. Application and evaluation of CO2 miscible flooding in extra-low permeability beach-bar sand reservoirs[J]. Petroleum Geology and Recovery Efficiency, 2020, 27(3): 113-119. https://www.cnki.com.cn/Article/CJFDTOTAL-YQCS202003016.htm [5] 仉莉. 降低CO2驱油最小混相压力化学体系研发[J]. 油气地质与采收率, 2020, 27(1): 45-49. https://www.cnki.com.cn/Article/CJFDTOTAL-YQCS202001007.htmZHANG Li. Development of chemical system for reducing minimum miscible pressure during CO2 flooding[J]. Petroleum Geology and Recovery Efficiency, 2020, 27(1): 45-49. https://www.cnki.com.cn/Article/CJFDTOTAL-YQCS202001007.htm [6] 李泽农, 黄秀祯, 张大夫, 等. 油田开发规划优选模型研究[J]. 石油学报, 1987, 8(4): 76-83.LI Zhenong, HUANG Xiuzhen, ZHANG Dafu, et al. Research of optimal development planning model for oilfield[J]. Acta Petrolei Sinica, 1987, 8(4): 76-83. [7] GOTTFRIED B S. Optimization of a cyclic steam injection process using penalty functions[J]. Society of Petroleum Engineers Journal, 1972, 12(1): 13-20. [8] LEE A S, ARONOFSKY J S. A linear programming model for scheduling crude oil production[J]. Journal of Petroleum Technology, 1958, 10(7): 51-54. [9] SLIDER H C. Practical petroleum reservoir engineering methods: an energy conservation science[M]. Tulsa: Petroleum Publishing Company, 1976. [10] 陈元千, 陶自强. 高含水期水驱曲线的推导及上翘问题的分析[J]. 断块油气田, 1997, 4(3): 19-24. https://www.cnki.com.cn/Article/CJFDTOTAL-DKYT199703005.htmCHEN Yuanqian, TAO Ziqiang. Derivation of water drive curve at high water-cut stage and its analysis of upwarping problem[J]. Fault-Block Oil & Gas Field, 1997, 4(3): 19-24. https://www.cnki.com.cn/Article/CJFDTOTAL-DKYT199703005.htm [11] 李立峰, 滕世婷, 冯绪波, 等. 基于水驱开发全过程的新型水驱特征曲线[J]. 特种油气藏, 2019, 26(3): 85-88. https://www.cnki.com.cn/Article/CJFDTOTAL-TZCZ201903015.htmLI Lifeng, TENG Shiting, FENG Xubo, et al. A new water-flooding characteristic curve based on the whole water-flooding process[J]. Special Oil & Gas Reservoirs, 2019, 26(3): 85-88. https://www.cnki.com.cn/Article/CJFDTOTAL-TZCZ201903015.htm [12] 赵永胜, 黄秀祯. 递减曲线的多功能预测模型[J]. 石油勘探与开发, 1985(5): 58-62. https://www.cnki.com.cn/Article/CJFDTOTAL-SKYK198505008.htmZHAO Yongsheng, HUANG Xiuzhen. A multiple functional model of decline curves[J]. Petroleum Exploration and Development, 1985(5): 58-62. https://www.cnki.com.cn/Article/CJFDTOTAL-SKYK198505008.htm [13] 陈元千, 郭二鹏. 新型油田产量递减模型的建立与应用[J]. 中国海上油气, 2008, 20(6): 379-381. https://www.cnki.com.cn/Article/CJFDTOTAL-ZHSD200806007.htmCHEN Yuanqian, GUO Erpeng. Building and applying a new decline model of oilfield production[J]. China Offshore Oil and Gas, 2008, 20(6): 379-381. https://www.cnki.com.cn/Article/CJFDTOTAL-ZHSD200806007.htm [14] 齐亚东, 王军磊, 庞正炼, 等. 非常规油气井产量递减规律分析新模型[J]. 中国矿业大学学报, 2016, 45(4): 772-778. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGKD201604016.htmQI Yadong, WANG Junlei, PANG Zhenglian, et al. A novel empirical model for rate decline analysis of oil and gas wells in unconventional reservoirs[J]. Journal of China University of Mining & Technology, 2016, 45(4): 772-778. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGKD201604016.htm [15] 高文君, 刘致远, 薛龙龙. 利用反向推理方法确定水驱特征曲线渗流方程[J]. 断块油气田, 2020, 27(4): 478-483. https://www.cnki.com.cn/Article/CJFDTOTAL-DKYT202004016.htmGAO Wenjun, LIU Zhiyuan, XUE Longlong. Determination of seepage equation of water drive characteristic curve by reverse derivation method[J]. Fault-Block Oil and Gas Field, 2020, 27(4): 478-483. https://www.cnki.com.cn/Article/CJFDTOTAL-DKYT202004016.htm [16] 李承龙, 迟博. 一种新型二氧化碳驱特征曲线的建立与应用[J]. 特种油气藏, 2020, 27(2): 98-102. https://www.cnki.com.cn/Article/CJFDTOTAL-TZCZ202002015.htmLI Chenglong, CHI Bo. A new characteristic curve of CO2 flooding and its application[J]. Special Oil & Gas Reservoirs, 2020, 27(2): 98-102. https://www.cnki.com.cn/Article/CJFDTOTAL-TZCZ202002015.htm [17] 谷建伟, 任燕龙, 张以根, 等. 一种改进的乙型水驱特征曲线研究及应用[J]. 特种油气藏, 2020, 27(1): 102-107. https://www.cnki.com.cn/Article/CJFDTOTAL-TZCZ202001015.htmGU Jianwei, REN Yanlong, ZHANG Yigen, et al. Research and application of an improved type-B water-flooding characteristic curve[J]. Special Oil & Gas Reserviors, 2020, 27(1): 102-107. https://www.cnki.com.cn/Article/CJFDTOTAL-TZCZ202001015.htm [18] 王柏力, 冯乔, 江海英, 等. 水驱特征曲线在低渗透油藏开发中的应用[J]. 特种油气藏, 2019, 26(6): 82-87. https://www.cnki.com.cn/Article/CJFDTOTAL-TZCZ201906015.htmWANG Baili, FENG Qiao, JIANG Haiying, et al. Application of waterflooding characteristic curve in the development of low-permeabilityoil reservoir[J]. Special oil & Gas Reservoirs, 2019, 26(6): 82-87. https://www.cnki.com.cn/Article/CJFDTOTAL-TZCZ201906015.htm [19] 代平, 孙良田, 李闽. 低渗透砂岩储层孔隙度、渗透率与有效应力关系研究[J]. 天然气工业, 2006, 26(5): 93-95. https://www.cnki.com.cn/Article/CJFDTOTAL-TRQG200605031.htmDAI Ping, SUN Liangtian, LI Min. Study on relation between porosity/permeability and effective stress of sand reservoir with low permeability[J]. Natural Gas Industry, 2006, 26(5): 93-95. https://www.cnki.com.cn/Article/CJFDTOTAL-TRQG200605031.htm [20] 傅建斌. 异常高压致密砂砾岩油藏开发机理及开发方式研究[D]. 青岛: 中国石油大学(华东), 2016.FU Jianbin. Research on mechanism and development mode of abnormally high pressure tight sandy conglomerate reservoir[D]. Qingdao: China University of Petroleum (East China), 2016. [21] 王敬, 刘慧卿, 刘仁静, 等. 考虑启动压力和应力敏感效应的低渗、特低渗油藏数值模拟研究[J]. 岩石力学与工程学报, 2013, 32(S2): 3317-3327. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2013S2043.htmWANG Jing, LIU Huiqing, LIU Renjin, et al. Numerical simulation for low-permeability and extra-low permeability reservoirs with considering starting pressure and stress sensitivity effects[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(S2): 3317-3327. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2013S2043.htm [22] 徐立坤, 齐梅, 李云波, 等. 碳酸盐岩油藏多测试辅助单井历史拟合[C]//2019油气田勘探与开发国际会议论文集. 西安: 西安石油大学, 2019.XU Likun, QI Mei, LI Yunbo, et al. Multi-test assisted single-well history matching in carbonate reservoirs[C]//Proceedings of 2019 International Conference on Oil and Gas Field Exploration and Development. Xi'an: Xi'an Shiyou University, 2019. [23] 张洪辉. 提高低渗裂缝性油田历史拟合精度的方法标准研究[J]. 中国石油和化工标准与质量, 2017, 37(11): 95-96. https://www.cnki.com.cn/Article/CJFDTOTAL-HGBJ201711046.htmZHANG Honghui. Research on methods and standards to improve the accuracy of history fitting in low permeability fractured oilfields[J]. China Petroleum and Chemical Standard and Quality, 2017, 37(11): 95-96. https://www.cnki.com.cn/Article/CJFDTOTAL-HGBJ201711046.htm [24] 朱晓颖, 蔡高玉, 陈小平, 等. 概率论与数理统计[M]. 北京: 人民邮电出版社, 2016.ZHU Xiaoying, CAI Gaoyu, CHEN Xiaoping, et al. Probability theory and mathematical statistics[M]. Beijing: Posts & Telecom Press, 2016. [25] 耿站立, 姜汉桥, 李杰, 等. 正交试验设计法在优化注聚参数研究中的应用[J]. 西南石油大学学报, 2007, 29(5): 119-121. https://www.cnki.com.cn/Article/CJFDTOTAL-XNSY200705038.htmGENG Zhanli, JIANG Hanqiao, LI Jie, et al. Application of orthogonal test design methodology in optimal parameters of polymer flooding[J]. Journal of Southwest Petroleum University, 2007, 29(5): 119-121. https://www.cnki.com.cn/Article/CJFDTOTAL-XNSY200705038.htm [26] 袁迎中, 张烈辉, 何磊, 等. 注采比多元回归分析及合理注采比的确定[J]. 石油天然气学报(江汉石油学院学报), 2008, 30(1): 299-302. https://www.cnki.com.cn/Article/CJFDTOTAL-JHSX200801082.htmYUAN Yingzhong, ZHANG Liehui, HE Lei, et al. Multiple regression analysis and determination of reasonable injection-production ratio[J]. Journal of Oil and Gas Technology (Journal of Jianghan Petroleum Institute), 2008, 30(1): 299-302. https://www.cnki.com.cn/Article/CJFDTOTAL-JHSX200801082.htm 期刊类型引用(8)
1. 邢川衡，赵云斌，高智梁. 修正Arrington模型下油田可采储量自动预测方法. 化学工程与装备. 2025(03): 79-81+107 . 
百度学术2. 陈禹欣，赵婷，承宁，马俊修，杨升峰，李蕴哲. 玛湖地区致密砾岩油藏小井距水平井立体井网开发研究与应用. 特种油气藏. 2023(02): 122-127 . 百度学术3. 卢比，胡春锋，马军. 南川页岩气田压裂水平井井间干扰影响因素及对策研究. 油气藏评价与开发. 2023(03): 330-339 . 百度学术4. 苏映宏. 探明未开发储量可动潜力评价新方法及应用——以Y油藏为例. 石油实验地质. 2022(02): 331-336 . 
本站查看5. 胡燕. 石油储量升级效益评价方法研究. 石油实验地质. 2022(03): 530-534 . 本站查看6. 李军，闫相宾. 成熟探区勘探目标群油气期望价值评估方法. 石油实验地质. 2022(03): 545-551 . 本站查看7. 曹炜，鲜成钢，吴宝成，于会永，陈昂，申颍浩. 玛湖致密砾岩油藏水平井生产动态分析及产能预测——以玛131小井距立体开发平台为例. 新疆石油地质. 2022(04): 440-449 . 百度学术8. 王玉风，姬安召，张光生，陈占军. 致密气藏不对称裂缝偏心直井半解析模型及其渗流特征. 新疆石油地质. 2022(04): 425-432 . 百度学术其他类型引用(0)
-
下载:
百度学术
计量
- 文章访问数: 599
- HTML全文浏览量: 257
- PDF下载量: 53
- 被引次数: 8
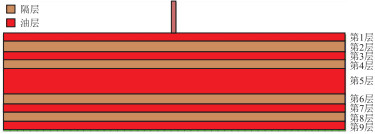
苏公网安备32021102000780号